Geometry dilations involve resizing figures by a scale factor while maintaining their shape. This concept is important in geometry as it helps to understand how objects can be transformed in size while preserving their proportions. Dilations are used in various mathematical applications, such as in mapping, architecture, and computer graphics.
When working with geometry dilations, it is crucial to understand the relationship between the original figure and its dilated image. The scale factor determines how much the figure will be enlarged or reduced. By practicing with geometry dilations worksheets, students can improve their understanding of this concept and strengthen their problem-solving skills.
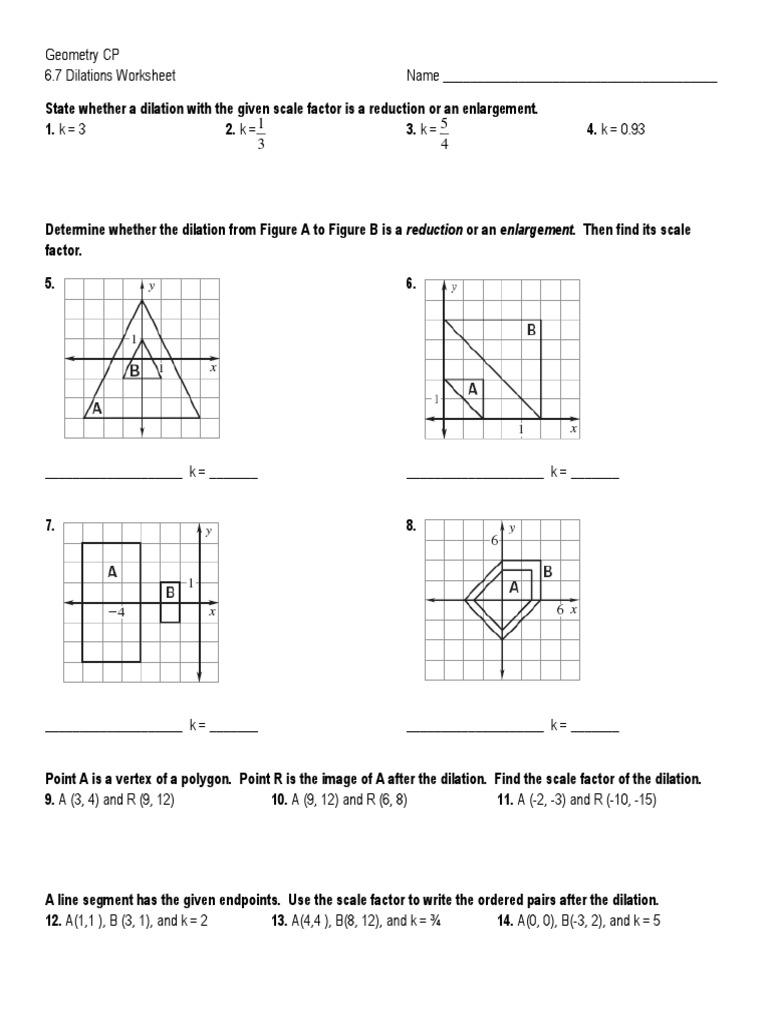
Geometry Dilations Worksheet
A geometry dilations worksheet typically consists of a series of exercises that require students to perform dilations on different figures. These exercises may involve dilating shapes both horizontally and vertically, as well as around a specific point. Students are required to calculate the scale factor and determine the coordinates of the dilated points.
Through these worksheets, students can practice applying the rules of dilations and develop their spatial reasoning skills. The exercises may vary in difficulty, allowing students to progress from basic dilations to more complex ones. By working through these worksheets, students can gain confidence in their ability to manipulate and transform geometric figures.
Geometry dilations worksheets also help students understand the real-world applications of this concept. By analyzing how dilations are used in various fields, such as architecture and art, students can see the practical relevance of geometry in everyday life. This can inspire them to explore further applications of dilations and deepen their understanding of geometry.
In conclusion, geometry dilations worksheets are valuable tools for students to practice and master the concept of resizing figures by a scale factor. By engaging with these worksheets, students can enhance their problem-solving skills, spatial reasoning, and understanding of geometric transformations. Through consistent practice and application, students can develop a strong foundation in geometry and apply their knowledge to real-world scenarios.