Geometry can be a challenging subject for many students, especially when it comes to proving lines parallel. However, with the right practice and resources, mastering this concept can become much easier. One effective way to improve understanding is by using proving lines parallel worksheets.
These worksheets typically contain various exercises and problems that require students to demonstrate their knowledge of parallel lines. By working through these worksheets, students can practice different methods of proving lines parallel and gain a better grasp of the concept.
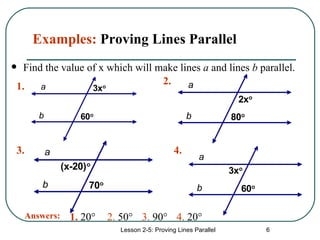
Proving Lines Parallel Worksheet
One common method of proving lines parallel is by using properties of angles. When two lines are intersected by a transversal, students can use angle relationships such as alternate interior angles, corresponding angles, or vertical angles to prove that the lines are parallel. By practicing these types of problems on a worksheet, students can become more comfortable with identifying and applying these angle relationships.
Another approach to proving lines parallel is by using theorems and postulates. For example, the Parallel Postulate states that if a transversal intersects two lines and the corresponding angles are congruent, then the lines are parallel. Students can practice applying this postulate on worksheets to solidify their understanding of when lines are parallel based on angle relationships.
Working through proving lines parallel worksheets also allows students to test their problem-solving skills and critical thinking abilities. By encountering different scenarios and challenges on the worksheets, students can develop their logical reasoning and analytical skills, which are essential for success in geometry and other mathematical subjects.
In conclusion, proving lines parallel worksheets are valuable tools for students to enhance their understanding of parallel lines and practice applying various methods of proof. By working through these worksheets, students can improve their problem-solving skills, strengthen their knowledge of geometry concepts, and ultimately feel more confident in their ability to prove lines parallel.